TOPOLOGIE - Topologie algébrique

TOPOLOGIE - Topologie algébrique

Inventée au début du XX^e siècle pour résoudre des problèmes géométriques, la topologie algébrique connut un grand développement grâce à l’introduction de constructions algébriques de plus en plus abstraites. Pour clarifier l’exposé, on a décomposé cet article en deux parties. Dans la première partie (chapitres 1 à 5), les problèmes géométriques sont traités d’une façon très concrète; dans la seconde partie (chapitres 6 et 7) sont rassemblées toutes les notions algébriques.

On emploiera les notations et abus de langage suivants.

«Espace» signifie «espace topologique» et «application» signifie «application continue».

Le segment [0, 1] de la droite réelle est noté I; un «arc joignant x à y dans l’espace X» est, par définition, une application de I dans X qui envoie 0 sur x et 1 sur y .

La boule unité de Rⁿ , pour la distance euclidienne, est notée Dⁿ ; son bord est la sphère S^{n -1}.

Si l’on a deux homomorphismes de groupes (ou de A-modules):

on dit que la suite:

est exacte si l’image de 見 est égale au noyau de 廓, soit Im 見 = Ker 廓, c’est-à-dire, si, pour un élément h de H, les deux conditions suivantes sont équivalentes:

a ) on a 廓(h ) = 0,

b ) il existe g dans G tel que 見(g ) = h .

On désigne par O le groupe (ou le A-module) réduit à son élément neutre; donc, la suite: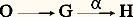

est exacte si et seulement si 見 est injectif; de même, la suite:

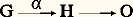est exacte si et seulement si 見 est surjectif.

1. Homotopie

À la notion banale de déformation continue des figures, on fait correspondre deux notions mathématiques. L’une, plus précise, est l’isotopie , qui sera définie et étudiée dans le chapitre 4 de l’article TOPOLOGIE - TOPOLOGIE DIFFÉRENTIELLE; l’autre, plus générale, est l’homotopie .

Applications homotopes

Deux applications f et g de l’espace X dans l’espace Y sont dites homotopes s’il existe une application h de X 憐 I dans Y telle que, pour tout point x de X, on ait h (x , 0) = f (x ) et h (x , 1) = g (x ). Cela définit, sur l’ensemble Hom(X, Y) des applications de X dans Y, une relation d’équivalence; les classes d’équivalence sont appelées les classes d’homotopie d’applications de X dans Y. Si X est un espace compact et Y un espace métrique et si l’on munit Hom(X, Y) de la topologie de la convergence uniforme (cf. TOPOLOGIE -Topologie générale, chap. 1), dire que f et g sont homotopes, c’est dire qu’il existe un arc 塚 dans Hom(X, Y) qui joint f à g : si h est l’homotopie, 塚(t ) est l’application de X dans Y qui à x associe h (x , t ).

Si A et B sont des sous-espaces de X et Y respectivement, une application f de X dans Y est appelée une application de (X, A) dans (Y, B) si elle applique A dans B. Deux applications f et g de (X, A) dans (Y, B) sont dites homotopes s’il existe une homotopie h de f à g , au sens de Hom(X, Y), telle que, pour tout t 捻 I, l’application x 料 h (x , t ) envoie A dans B, c’est-à-dire si f et g peuvent être joints par un chemin dans le sous-espace de Hom (X, Y) formé par les applications de (X, A) dans (Y, B). Si A et B sont des sous-espaces de A et B respectivement, une application de X dans Y qui applique A dans B et A dans B est appelée une application de (X, A, A ) dans (Y, B, B ); deux telles applications f et g sont dites homotopes s’il existe entre elles une homotopie, au sens de Hom(X, Y), telle que, pour tout t , l’application x 料 h (x , t ) envoie A dans B et A dans B .

Exemples

Deux applications f et g de X dans Rⁿ sont toujours homotopes, car on définit une homotopie h de f à g en posant:

où x 捻 X et t 捻 I.

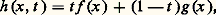Au contraire, deux applications f et g de X dans Rⁿ 漣O peuvent ne pas être homotopes. Par exemple, l’application constante f qui envoie S¹ sur le point (2, 0) et l’application naturelle g de S¹ dans R² 漣O ne sont pas homotopes: il existe des déformations de f à g dans R², mais elles rencontrent toutes O; ce ne sont donc pas des déformations parmi les applications de S¹ dans R² 漣O.

Type d’homotopie

En utilisant les notations de l’article CATÉGORIES ET FONCTEURS, on peut dire que la topologie algébrique est l’étude de la catégorie dont les objets sont les espaces topologiques et dont les morphismes sont les classes d’homotopie d’applications; donc, en topologie algébrique, on ne fera jamais la différence entre deux applications homotopes. Il en résulte que, si 﨏 : XY et 祥 : YX sont deux applications telles que 祥 獵 﨏 : XX soit homotope à l’application identique de X et que 﨏 獵 祥 : YY soit homotope à l’application identique de Y, les applications 﨏 et 祥 sont considérées comme des isomorphismes inverses l’un de l’autre. De telles applications sont appelées des équivalences d’homotopie; on dit encore que X et Y ont le même type d’homotopie . On étend facilement cette notion aux paires d’espaces. Un espace X est dit contractile s’il a le type d’homotopie de l’espace réduit à un point.

Par exemple, X = S¹ et Y = R² 漣O ont même type d’homotopie: on définit 﨏 par 﨏(x ) = x et 祥 par 祥(y ) = y / 瑩y 瑩; l’application 祥 獵 﨏 est l’identité de S¹ et 﨏 獵 祥 est homotope à l’identité de R² 漣O grâce à l’homotopie:

On montre facilement que Rⁿ et Dⁿ sont contractiles.

Le groupe de Poincaré

Soit x un point de l’espace topologique X. On suppose que X est connexe par arcs, c’est-à-dire que tout point y peut être joint à x par un arc; il en résulte que X est connexe. On note 神¹(X, x ) l’ensemble des classes d’homotopie d’applications de (I, face=F00190, 1) dans (X, x ). À tout couple (f , g ) d’applications de (I, face=F00190, 1) dans (X, x ) on associe l’application h : IX qui envoie t sur f (2t ), si t 諒 1/2, et sur g (2t 漣 1), si t 閭 1/2; on a h (0) = h (1) = x et la classe de h dans 神¹(X, x ) ne dépend que des classes de f et de g ; on a donc défini une loi de composition sur 神¹(X, x ). C’est une loi de groupe. L’élément neutre est la classe de l’application constante qui à tout t associe x . L’inverse de la classe de f : IX est la classe de l’application g définie par g (t ) = f (1 漣 t ). Ce groupe s’appelle le groupe de Poincaré , ou encore le premier groupe d’homotopie de (X, x ).

Si 﨏 est une application de (X, x ) dans (Y, y ) et si f est une application de (I, face=F00190, 1) dans (X, x ), alors 﨏 獵 f est une application de (I, face=F00190, 1) dans (Y, y ); sa classe d’homotopie ne dépend que de 﨏 et de celle de f . Cela définit un homomorphisme: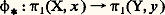

qui ne dépend que de la classe d’homotopie de 﨏 parmi les applications de (X, x ) dans (Y, y ). Si 祥 est une application de (Y, y ) dans (Z, z ), les deux homomorphismes 祥 獵 﨏 et ( 祥 獵 﨏) de 神¹(X, x ) dans 神¹(Z, z ) sont égaux; on exprime cela, dans le langage des catégories, en disant que le groupe de Poincaré est un foncteur de la catégorie des espaces topologiques pointés dans celle des groupes.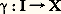

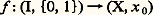Soit x ⁰ et x ¹ deux points de X et soit:

un arc qui joint x ⁰ à x ¹; à toute application:

on associe l’application:

définie par:

On obtient ainsi une application de 神¹(X, x ⁰) dans 神¹(X, x ¹), qui est un isomorphisme de groupes. Si x ⁰ = x ¹, c’est l’automorphisme intérieur défini par la classe d’homotopie de 塚. En particulier, si 神¹(X, x ) est nul pour un point x de X, il en est de même pour tous les autres points de X; on dit alors que X est simplement connexe .

Exemples

Soit s un point du cercle S¹; le groupe 神¹(S¹, s ) est isomorphe à 神¹(R² 漣O, s ) puisque S¹ et R² 漣O ont le même type d’homotopie et ces groupes sont isomorphes à Z, l’isomorphisme étant obtenu en comptant combien de fois chaque lacet: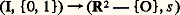

fait le tour de l’origine.

Les sphères Sⁿ , avec n 閭 2, sont simplement connexes: si l’on enlève un point à Rⁿ , on obtient un espace ayant le type d’homotopie de S^{n -1}: il est donc simplement connexe si n 閭 3.

Si l’on recolle (X, x ) et (Y, y ) en identifiant les points de base, on obtient un espace dont le groupe de Poincaré est isomorphe au produit libre de 神¹(X, x ) et 神¹(Y, y ).

Si l’on perce n trous dans un plan, on obtient un espace qui a le type d’homotopie de n cercles réunis par leurs points de base; son groupe de Poincaré est donc un groupe libre à n générateurs.

On montre que 神¹(X 憐 Y, (x , y )) est la somme directe de 神¹(X, x ) et de 神¹(Y, y ); en particulier, si t est un point du tore T² de la géométrie élémentaire, qui est le produit de deux cercles, alors 神¹(T², t ) est isomorphe à Z 簾 Z.

Revêtements

Soit x un point de l’espace connexe par arcs X. Un revêtement de (X, x ) est un triplet ((face="EU Acute" お, じ ), p ) où じ est un point de l’espace connexe お, et où p est une application de (face="EU Acute" お, じ ) dans (X, x ) qui vérifie la condition suivante.

Condition (R) . Pour tout point m de X, il existe un voisinage U et une partition de p ^-1(U) en sous-ensembles (Vⁱ ), i 捻 I, telle que, pour tout i , la restriction p ^|Vi de p à Vⁱ soit un homéomorphisme de Vⁱ sur U.

En d’autres termes, 神^-1(m ) est un sousensemble discret de お et il existe un voisinage U de M tel que 神^-1(U) soit homéomorphe au produit de 神^-1(m ) par U. Il n’en résulte pas que お est le produit de X par 神^-1(M); par exemple, l’application d’enroulement de R sur le cercle, qui associe au nombre le point de coordonnées (cos , sin ), définit un revêtement:

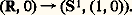Soit f une application de A dans お et 﨏 une application de A 憐 I dans X telles que:

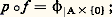alors il existe une application F de A 憐 I dans お, et une seule, telle que les deux conditions suivantes soient satisfaites:

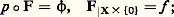c’est le principe du relèvement des homotopies . On en déduit que l’homomorphisme:

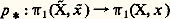est injectif.

Si tout point de X possède un voisinage contractile, parmi les revêtements de (X, x ) il en existe un qui est simplement connexe; on l’appelle le revêtement universel . Pour tout point y de X, notons F^y l’ensemble des classes d’homotopie d’applications de (I, 0, 1) dans (X, x , y ); le revêtement universel est obtenu en munissant la réunion de tous les F^y d’une topologie convenable. On fait opérer 神¹(X, x ) sur le revêtement universel en associant à g 捻 神¹(X, x ) et à 見 捻 F^y l’élément 廓 de F^y obtenu en mettant bout à bout une application de (I, (0, 1)) dans (X, x ) qui représente g et une application de (I, 0, 1) dans (X, x , y ) qui représente 見. Si G est un sous-groupe de 神¹(X, x ), l’espace quotient de l’action de G sur le revêtement universel est un revêtement de (X, x ); on montre que tout revêtement est de cette forme. Cela donne donc une classification complète des classes à isomorphisme près des revêtements de (X, x ). Par exemple, les revêtements du cercle sont, outre le revêtement universel:

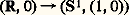d’enroulement de R sur le cercle déjà cité, les applications:

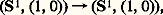définies par:

où p est entier strictement positif.

Groupes d’homotopie

Pour tout espace X et pour tout point x de X, on note 神ⁿ (X, x ) l’ensemble des classes d’homotopie d’applications de (Dⁿ , S^{n -1}) dans (X, x ). Découpons Dⁿ en deux demi-boules D⁺ⁿ et D^-n et choisissons des homéomorphismes orientés 﨏⁺ et 﨏^- de Dⁿ sur chacune d’elles; à tout couple (f , g ) d’applications de (Dⁿ , S^{n -1}) dans (X, x ) on en associe une troisième, définie comme étant f 獵 﨏^+-1 sur D⁺ⁿ et f 獵 﨏^—1 sur D^-n . Par passage aux classes d’homotopie, cela définit sur 神ⁿ (X, x ) une structure de groupe: c’est le n -ième groupe d’homotopie de (X, x ); pour n = 1, on retrouve le groupe de Poincaré; pour n 閭 2, ce groupe est commutatif.

On définit, pour n 閭 2, le n -ième groupe d’homotopie de (X, A, x ), où x 捻 A 說 X, en munissant d’une loi de groupe l’ensemble 神ⁿ (X, A, x ) des classes d’homotopie de (Dⁿ , S^{n -1}, S^{+n -1}) dans (X, A, x ), grâce à une construction géométrique analogue à la précédente.

Chaque fois que x est un point du sous-espace A de X, on a un homomorphisme: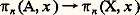

induit par l’inclusion; mais on a aussi un homomorphisme:

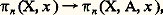car une application de (Dⁿ , S^{n -1}) dans (X, x ) est aussi une application de (Dⁿ , S^{n -1}, S^{+n -1}) dans (X, A, x ); on a également un homomorphisme:

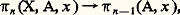obtenu en prenant la restriction au couple (S^{-n -1}, S^{n -2}), qui est homéomorphe au couple (D^{n -1}, S^{n -2}), des applications de (Dⁿ , S^{n -1}, S^{+n -1}) dans (X, A, x ). On vérifie que la suite:

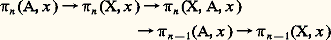est exacte pour tout n 閭 2.

Les groupes d’homotopie donnent des renseignements assez complets sur le type d’homotopie (cf. chap. 1). Leur calcul est malheureusement très difficile. On ne connaît pas les groupes d’homotopie des sphères: on sait que 神ⁱ (Sⁿ , s ) est nul pour i 麗 n et que 神ⁿ (Sⁿ , s ) est isomorphe à Z; à part cela, on ne connaît les 神ⁱ (Sⁿ , s ) que pour n , i ou i 漣 n assez petit.

2. Ensemble simpliciaux et polyèdres

Nous avons dit que l’objet de la topologie algébrique était l’étude des propriétés homotopiques des espaces topologiques; en fait, ce projet est trop ambitieux: on ne sait que peu de chose des espaces les plus généraux. Mais il existe cependant des classes assez larges d’espaces topologiques pour lesquelles cette étude peut être menée assez loin; l’une des plus intéressantes est celle des polyèdres.

La notion de simplexe

On appelle simplexe type de dimension n et on note ⁿ le sous-espace de R^{n +1} formé des points dont les coordonnées (x ⁰, ..., x ⁿ ) vérifient les deux relations:

pour tout i . En particulier, ⁰ est le point 1 de R, ¹ est le segment qui joint les points (0, 1) et (1, 0) de R², ² est un triangle et ³ est un tétraèdre.

Soit E^p un sous-espace vectoriel de R^{n +1} qui est engendré par p + 1 des vecteurs de la base naturelle de R^{n +1}; alors ⁿ 惡 E^p est homéomorphe au simplexe type de dimension p : on dit que c’est une face de dimension p de ⁿ ; les faces de dimension zéro sont appelées des sommets .

Les simplexes affines de R^N

Pour tout ensemble ordonné 靖 = (s ⁰, ..., s ⁿ ) de points de R^N, qui a n + 1 éléments, on notera [ 靖] l’enveloppe convexe de 靖, c’est-à-dire l’ensemble des points de R^N qui peuvent s’écrire: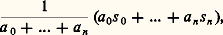

avec des coefficients a ⁱ tous positifs ou nuls et tels que a ⁰ + ... + a ⁿ 礪 0. On note 﨏 size=1^靖 l’application linéaire de R^{n +1} dans R^N qui, pour tout i , applique le i -ème vecteur de la base naturelle de R^{n +1} sur s ⁱ . Il est clair que 﨏 size=1^靖 applique ⁿ sur [ 靖] et que la restriction de 﨏 size=1^靖 à ⁿ est un homéomorphisme de ⁿ sur [ 靖] si et seulement si les n vecteurs s ¹ 漣 s ⁰, ..., s ⁿ 漣 s ⁰ sont indépendants, c’est-à-dire si les points de 靖 ne sont pas contenus dans un sous-espace affine de dimension strictement inférieure à n . Dans la suite, on supposera que cette condition est vérifiée et on dira que [ 靖] est un n -simplexe affine de R^N. Pour tout sous-ensemble 靖 de 靖, l’enveloppe convexe [ 靖 ] est appelée une face de [ 靖]; les points de 靖 sont appelés les sommets de [ 靖]. L’application 﨏 size=1^靖 définit des homéomorphismes des faces de ⁿ sur celles de [ 靖].

Complexes simpliciaux

Considérons un sous-ensemble 崙⁰ discret de R^N et une famille 崙 de parties finies de 崙⁰; on suppose que:

見) tout élément 靖 de 崙 définit un simplexe affine;

廓) toute partie de 崙⁰ ayant un seul élément est dans 崙;

塚) toute partie d’un élément de 崙 est dans 崙;

嗀) pour tout couple ( 靖, 靖 ) d’éléments de 崙, on a:

Notons X la réunion de tous les simplexes [ 靖] pour 靖 捻 崙; c’est un sous-espace fermé de R^N. Les simplexes [ 靖], avec 靖 捻 崙, sont tracés sur X et on dit qu’ils forment une triangulation [ 崙] de X.

Un tel espace triangulé X est encore appelé un complexe simplicial . La propriété 廓, imposée à 崙, entraîne que 崙⁰ 說 X; on voit que 崙⁰ est l’ensemble des sommets de [ 崙], que toute face d’un simplexe de [ 崙] est un simplexe de [ 崙] et que, si deux simplexes de [ 崙] ne sont pas disjoints, leur intersection est l’une de leurs faces, éventuellement égale à l’un d’eux.

Par exemple, ⁿ est un complexe simplicial dont les simplexes sont ⁿ lui-même et toutes ses faces; une ligne brisée est un complexe simplicial n’ayant des simplexes qu’en dimension zéro et un; en découpant chacune de ses faces en deux triangles, on fait du bord d’un cube un complexe simplicial (cf. figure).

Applications simpliciales

Soit [ 靖] un simplexe affine de R^N et [ 精] un simplexe affine de R^P. Toute application de l’ensemble fini 靖 dans l’ensemble fini 精 se prolonge, de façon unique, en une application de [ 靖] dans [ 精] qui est la restriction à [ 靖] d’une application affine de R^N dans R^P; une telle application de [ 靖] dans [ 精] est dite affine . Soit (X, [ 崙]) et (Y, [ 淪]) deux complexes simpliciaux; une application continue f de X dans Y est dite affine si la restriction de f à [ 靖], pour tout simplexe [ 靖] de [ 崙], est une application affine de [ 靖] dans un simplexe de [ 淪]. Deux applications affines f et g de (X, [ 崙]) dans (Y, [ 糖]) sont dites contiguës si, pour tout simplexe [ 靖] de [ 崙], les ensembles f ([ 靖]) et g ([ 靖]) sont des faces d’un même simplexe de [ 淪].

On démontre que toute application continue de X dans Y est homotope à une application simpliciale et que, si X est compact, on peut à tout couple (f , g ) d’applications simpliciales homotopes de (X, [ 崙]) dans (Y, [ 淪]) associer une suite finie f ⁰ = f , f ¹, ..., f ^k = g d’applications simpliciales telles que, pour tout i , les applications f ^-1 et f ⁱ soient contiguës.

Étant donné qu’une application simpliciale est entièrement déterminée par les images des sommets de [ 崙], il est clair que la détermination des classes d’homotopie de X dans Y est ramenée à un problème combinatoire, fini si X est compact.

Polyèdres

Si un sous-espace X de R^N peut être triangulé comme on vient de l’indiquer (cf. Complexes simpliciaux ), on dit que c’est un polyèdre plongé dans R^N. Un polyèdre peut être triangulé de plusieurs façons: on dit que la triangulation [ 淪] est une subdivision de la triangulation [ 崙] si l’ensemble des sommets de [ 淪] contient l’ensemble des sommets de [ 崙]; il en résulte que tout simplexe de [ 淪] est contenu dans un simplexe de [ 崙]. Deux triangulations du même polyèdre plongé dans R^N ont toujours une subdivision commune. Une application continue du polyèdre X dans le polyèdre Y est dite semi-linéaire si elle devient simpliciale pour des choix convenables des triangulations de X et de Y.

3. Homologie singulière

Entiers d’incidence

Dans ce chapitre, on fixe, une fois pour toutes, pour tout n 閭 2, une orientation de Dⁿ et de S^{n - 1} (cf. VARIÉTÉS DIFFÉRENTIABLES, chap. 2). Soit [ 靖] un n -simplexe affine, et soit d [ 靖] la réunion de ses faces, de dimension au plus égale n 漣 1; le couple ([ 靖], d [ 靖]) est homéomorphe à (Dⁿ , S^{n - 1}); orienter [ 靖] c’est choisir une classe d’homéomorphismes de Dⁿ sur [ 靖] qui définissent des homéomorphismes de S^{n - 1} sur d [ 靖]; chaque face [ 靖 ] de dimension n 漣 1 de [ 靖] est alors identifiée à un morceau de S^{n - 1} et elle est donc orientée. C’est l’orientation induite sur [ 靖 ] par l’orientation de [ 靖].

Considérons maintenant un complexe simplicial (X, [ 崙]) et orientons chacun de ses simplexes de dimension strictement positive. Pour toute face [ 靖 ] de dimension n 漣 1 du n -simplexe [ 靖], avec n 閭 2, on a donc deux orientations, celle que l’on a choisie et celle qui est induite par l’orientation de [ 靖]. On définit un nombre entier 﨎 size=1^靖/ size=1^靖 size=1, appelé entier d’incidence de [ 靖 ] par rapport à [ 靖], de la façon suivante: on a 﨎 size=1^靖/ size=1^靖 size=1 = 1 si ces deux orientations coïncident, et 﨎 size=1^靖/ size=1^靖 size=1 = 漣 1 si ces deux orientations diffèrent. Si [ 靖] est un 1-simplexe, son orientation est une classe d’homéomorphismes de D¹ = [ 漣 1, + 1] sur [ 靖]; elle identifie l’une des deux faces de dimension zéro, c’est-à-dire l’un des sommets de [ 靖], à + 1 (pour cette face [ 靖 ], on pose 﨎 size=1^靖/ size=1^靖 size=1 = 1) et l’autre à 漣 1 (pour cette face [ 靖 ], on pose 﨎 size=1^靖/ size=1^靖 size=1 = 漣 1).

Cycles et homologie

Soit A un anneau unitaire; on notera Cⁿ (face=F0021 崙, A) le A-module libre dont la base est l’ensemble des n -simplexes de la triangulation [ 崙]. Un élément de Cⁿ (face=F0021 崙, A) est appelé une n -chaîne du complexe simplicial (X, [ 崙]); c’est une expression formelle 見 size=1^靖 靖, où [ 靖] parcourt l’ensemble des n -simplexes de [ 崙] et où tous les 見 size=1^靖, à l’exception d’un nombre fini, sont nuls. À tout n -simplexe [ 靖] on associe une (n 漣 1)-chaîne d ⁿ 靖, appelée son bord , définie par:

où [ 靖 ] parcourt l’ensemble des faces de dimension n 漣 1 de 靖. On étend d ⁿ en un homomorphisme de Cⁿ (face=F0021 崙, A) dans C^{n - 1}(face=F0021 崙, A), que l’on appelle encore le bord, en posant: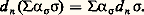

On démontre que, pour tout simplexe [ 靖] et pour tout couple ([ 靖 ], [ 靖 ]) de faces de codimension 1 de [ 靖] qui se coupent suivant [ 靖], on a:

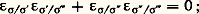il en résulte que d ⁿ d ^{n + 1} = 0.

Les n -chaînes u telles que d ⁿ u = 0 sont appelées les cycles de dimension n du complexe simplicial (X, [ 崙]). Deux cycles de dimension n sont dits homologues si leur différence est le bord d’une (n + 1)-chaîne. Il est clair que les cycles de dimension n forment un sous-A-module de Cⁿ (face=F0021 崙, A) et que l’ensemble de leurs classes modulo l’homologie en est un module quotient; on le note Hⁿ (face=F0021 崙, A). En employant les définitions algébriques du chapitre 6, on peut dire qu’en posant Cⁿ (face=F0021 崙, A) = 0, pour n 麗 0, on obtient un A-module différentiel gradué face=F9796 C(face=F0021 崙, A) dont le n -ième groupe d’homologie est Hⁿ (face=F0021 崙, A).

À toute application simpliciale f de (X, [ 崙]) dans (Y, [ 淪]) on associe un homomorphisme f ⁿ de Cⁿ (face=F0021 崙, A) dans Cⁿ (face=F0021 淪, A) en posant, pour tout n -simplexe [ 靖] de [ 崙], ou bien:

si f ^|[ size=1^靖] est un homéomorphisme de 靖 sur un simplexe de dimension n de 淪 (avec le signe + s’il conserve l’orientation et le signe 漣 s’il la change), ou bien: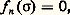

si f ([ 靖]) est un simplexe de dimension strictement inférieure à n . Les f ⁿ forment un homomorphisme de module différentiel de face=F9796 C(face=F0021 崙, A) dans face=F9796 C(face=F0021 淪, A) qui induit sur les homologies des homomorphismes:

On démontre que, si f et g sont contiguës, alors f et g coïncident. Il en résulte que:

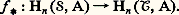a ) si 﨏 est une application continue de X dans Y, toutes les approximations simpliciales de 﨏 induisent le même homomorphisme de Hⁿ (face=F0021 崙, A) dans Hⁿ (face=F0021 淪, A); cet homomorphisme sera noté 﨏;

b ) si 崙 est une autre triangulation de l’espace topologique X, l’application identique de X induit un isomorphisme de Hⁿ (face=F0021 崙, A) sur Hⁿ (face=F0021 崙 , A); donc Hⁿ (face=F0021 崙, A) ne dépend que de l’espace topologique X et non de la triangulation 崙 choisie; c’est pourquoi, à partir de maintenant, on le notera Hⁿ (X, A);

c ) si 﨏 et 祥 sont deux applications homotopes de X dans Y, elles induisent le même homomorphisme de Hⁿ (X, A) dans Hⁿ (Y, A); en particulier, Hⁿ (X, A) ne dépend que du type d’homotopie de X.

Les nombres de Betti de X (définis par Poincaré) sont les dimensions b ⁿ des espaces vectoriels Hⁿ (X, Q); les nombres de Betti modulo p , avec p entier premier, sont les dimensions des espaces vectoriels Hⁿ (X, Z/p Z). La somme alternée:

est appelée la caractéristique d’Euler-Poincaré . Si X est triangulé et s’il a 見ⁿ simplexes de dimension n , on a: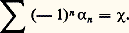

Homologie relative

Soit X un sous-complexe de (X, [ 崙]), c’est-à-dire un fermé de X qui est une réunion de simplexes de [ 崙]. Pour tout n , le module Cⁿ (face=F0021 崙|X , A) est un sous-A-module de Cⁿ (face=F0021 崙, A); l’homologie du groupe différentiel quotient ne dépend pas de la triangulation [ 崙] choisie; c’est l’homologie relative de X modulo X ; on la note Hⁿ (X, X ; A), avec n 閭 0. Un cycle relatif est une chaîne de X dont le bord est dans X ; deux cycles relatifs de dimension n sont homologues si leur différence est la somme d’une n -chaîne de X et du bord d’une (n + 1)-chaîne de X.

Tout cycle de X est un cycle relatif; on en déduit des applications:

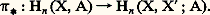Le bord d’un cycle relatif de dimension n est un cycle de dimension n 漣 1 de X ; on en déduit des applications:

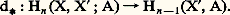On démontre que, pour tout n , la suite:

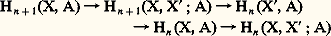est exacte; c’est un cas particulier de la suite exacte décrite au chapitre 6.

À toute application du complexe simplicial X dans le complexe simplical Y qui envoie le sous-complexe X dans le sous-complexe Y on associe, par une méthode analogue à celle que l’on a utilisée pour le cas absolu, des applications:

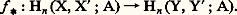Principe d’excision . Si Y et Z sont deux sous-complexes de X, les deux modules quotients:

sont identiques; on en déduit que l’application: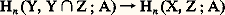

déduite de l’injection de (Y, Y 惡 Z) dans (X, Z) est un isomorphisme; c’est ce qu’on appelle le principe d’excision. L’homologie relative de X modulo Z ne dépend donc que des points de X 漣 Z et des points de Z qui sont voisins de X 漣 Z.

Exemples

1. Homologie d’un point . Un point x ⁰ est un complexe simplicial ayant un seul simplexe de dimension zéro; donc Cⁱ (x ⁰, A) est nul pour i non nul et est isomorphe à A si i est nul; tous les opérateurs bord sont évidemment nuls. Donc on a:

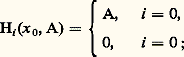c’est aussi l’homologie de tous les espaces contractiles.

2. Le calcul de H⁰. Le module d’homologie H⁰(X, A) est le conoyau de l’homomorphisme:

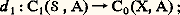une 0-chaîne de la forme 靖⁰ 漣 靖¹ est un bord si et seulement si il existe un arc dans X qui joint le point 靖⁰ au point 靖¹. On en déduit que, si X est connexe, alors H⁰(X, A) est isomorphe à A. Si le complexe simplicial X n’est pas connexe, il est réunion de sous-complexes connexes disjoints; ces sous-complexes sont appelés les composantes connexes de X; la composante connexe qui contient le point x est l’ensemble des points de X qui peuvent être joints à x par un arc; H⁰(X, A) est le A-module libre dont la base est l’ensemble des composantes connexes de X.

3. Homologie du cercle S¹. Le cercle est homéomorphe au bord du simplexe type ²; c’est un complexe simplicial ayant trois 0-simplexes et trois 1-simplexes; donc Cⁱ est nul pour i différent de 0 et de 1, et C⁰ et C¹ sont isomorphes à A 簾 A 簾 A. L’homomorphisme d ¹ (c’est-à-dire le seul opérateur bord non nul) est donné par la matrice:

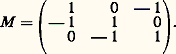Les seuls modules d’homologie non nuls sont donc H⁰(S¹, A) et H¹(S¹, A), qui sont le noyau et le conoyau de d ¹ et sont, par conséquent, isomorphes à A.

4. Homologie des sphères . On démontre les égalités suivantes:

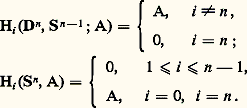Théorèmes de Whitehead et de Hurewicz

Pour définir le type d’homotopie d’un espace X, il ne suffit pas de donner ses groupes d’homotopie; cependant, si f est une application du polyèdre connexe X dans le polyèdre connexe Y qui, pour tout i 礪 0, induit un isomorphisme de 神ⁱ (X, x ⁰) sur 神ⁱ (Y, f (x ⁰)), alors f est une équivalence d’homotopie. De même, deux espaces peuvent avoir même homologie sans être homotopiquement équivalents; mais, si f est une application du polyèdre connexe X dans le polyèdre connexe Y qui induit un isomorphisme de Hⁱ (X, Z) sur Hⁱ (Y, Z), pour i 諒 n , et si X et Y sont simplement connexes, alors f induit un isomorphisme de 神ⁱ (X, x ⁰) sur 神ⁱ (Y, f (x ⁰)), pour i 諒 n ; c’est le théorème de Whitehead.

Il en résulte que, si l’application f du polyèdre X dans le polyèdre Y induit, pour tout i , un isomorphisme de Hⁱ (X, Z) sur Hⁱ (Y, Z) et si X et Y sont connexes et simplement connexes, alors f est une équivalence d’homotopie; en particulier, tout polyèdre simplement connexe qui a l’homologie du point est contractile; il existe cependant des espaces non simplement connexes, donc non contractiles, qui ont l’homologie du point.

On voit qu’il existe des rapports étroits entre l’homologie et les groupes d’homotopie d’un espace. C’est ce que précise le théorème de Hurewicz qui affirme:

a ) Pour tout espace connexe X, le groupe H¹(X, Z) est le quotient de 神¹(X, x ⁰) par le sous-groupe engendré par ses commutateurs;

b ) Pour tout espace X connexe et simplement connexe tel que 神ⁱ (X, x ⁰) soit nul pour i 麗 n , alors Hⁱ (X, Z) est égal à 神ⁱ (X, x ⁰) pour i 諒 n .

4. Les espaces fibrés

Fibrés localement triviaux

Soit 﨏: YB une application et soit F un espace topologique. Supposons que, pour tout point b de B, l’ensemble 﨏^-1(b ) soit homéomorphe à F; on dit alors que 﨏: YB est un fibré de fibre F et de base B. L’ensemble 﨏^-1(b ) est appelé la fibre du point b .

Un exemple de cette situation est le cas où Y = F 憐 B et où 﨏 est la seconde projection du produit Y 憐 B; ce fibré est appelé le fibré trivial de fibre F et de base B.

Pour tout sous-espace B de B et pour tout fibré 﨏: YB de fibre F,

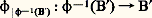est encore un fibré de fibre F. On dit que 﨏: YB est un fibré localement trivial si chaque point b de B posède un voisinage U tel que:

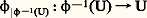soit isomorphe au fibré trivial (c’est-à-dire tel qu’il puisse exister un homéomorphisme 兀 : 﨏^-1(U)F 憐 U tel que, pour tout point y de 﨏^-1(U), le point 﨏(y ) soit la seconde projection de 兀(y )).

Citons deux exemples de fibrés localement triviaux.

1. Soit B une variété différentiable de dimension n et soit Y la variété de ses vecteurs tangents. En associant à tout vecteur tangent son point de contact, on peut définir un fibré 﨏 : YB qui a pour fibre Rⁿ ; il est localement trivial, car, pour tout ouvert de coordonnées U de B,

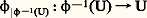est isomorphe au fibré trivial.

2. Soit G un groupe topologique et soit G un sous-groupe fermé. Notons 﨏 l’application naturelle de G sur l’ensemble des classes à droite G/G ; c’est une fibration de fibre G . Si G est un groupe de Lie et G un sous-groupe de Lie, ce fibré est localement trivial. Les groupes classiques (cf. GROUPES -Groupes classiques et géométrie) donnent de multiples exemples de cette construction; par exemple, si on a G = SO(3) et G = SO(2), qui sont les groupes des rotations dans R³ et dans R² respectivement, G/G est la sphère S² et 﨏: GG/G est l’application qui à g 捻 SO(3) associe l’image par g du vecteur (1, 0, 0) de R³.

Considérons maintenant un fibré localement trivial 﨏: YB de fibre F, deux ouverts B⁰ et B¹ et soit deux trivialisations:

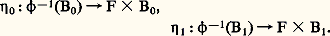L’application 兀⁰ 獵 兀^1-1 de F 憐 (B⁰ 惡 B¹) dans lui-même commute avec la projection sur B⁰ 惡 B¹; elle définit une application de B⁰ 惡 B¹ dans le groupe des homéomorphismes de F et cette application est continue si on munit ce groupe d’une topologie appropriée. En général, on se donne un sous-groupe H de ce groupe d’homéomorphismes et des trivialisations 兀ⁱ telles que les homéomorphismes de F donnés par les applications 兀ⁱ 獵 兀^{j -1} soient dans H; on dit alors que H est le groupe structural du fibré. Par exemple, le groupe structural du fibré des vecteurs tangents à une variété de dimension n est le groupe GL(n ) des matrices réelles d’ordre n inversibles, puisque les applications 兀ⁱ 獵 兀^{j -1} sont données par les différentielles des changements de cartes de la variété. Si la variété est orientable, ces différentielles ont toutes un déterminant positif; donc le groupe structural est le sous-groupe GL⁺(n ) de GL(n ) formé des matrices à déterminant positif.

Dans le cas où la fibre est un groupe, il se peut que le groupe structural soit la fibre elle-même, opérant par translation à droite; on dit alors qu’on a un fibré principal . C’est le cas du fibré 﨏: GG/G ; c’est aussi le cas du revêtement universel de (X, x ), le groupe structural étant alors le groupe discret 神¹(X, x ).

La suite exacte d’homotopie d’un fibré

Choisissons un point y dans Y et posons 﨏(y ) = b ; l’application:

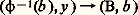et l’application d’inclusion:

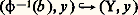induisent sur les groupes d’homotopie des applications:

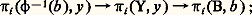un élément de 神ⁱ (B, b ) peut être représenté par une application 兀 de (Dⁱ , S^{i -1}) dans (B, b ). On montre que, pour tout point s de S^{i -1}, il existe une application 猪 de (Dⁱ , S^{i -1}, s ) dans (Y, 﨏^-1(b ), y ) telle que 﨏 獵 猪 = 兀. La restriction de 猪 à S^{i -1} définit un élément de 神^{i -1}( 﨏^-1(b ), y ); on obtient ainsi un homomorphisme de 神ⁱ (B, b ) dans 神^{i -1}( 﨏^-1(b ), y ). On démontre que, compte tenu de l’identification de 﨏^-1(b ) avec F, on a ainsi défini, pour tout i 閭 1, une suite exacte:

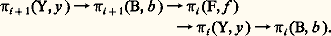Homologie d’un espace fibré

Quand on connaît l’homologie de la base et l’homologie de la fibre d’un fibré localement trivial 﨏: YB, on a d’assez bons renseignements sur l’homologie de Y, puisque, si B est simplement connexe, il existe une suite spectrale (cf. Suites spectrales , in chap. 6), dont le terme E² est l’homologie de B à coefficients dans l’homologie de F, qui converge vers l’homologie de Y.

Pour tout espace A où l’on a choisi un point a , on note SA l’espace obtenu à partir de A 憐 I en contractant:

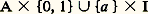en un point a ¹; c’est la suspension de A. On peut itérer cette construction n fois pour obtenir le n -ième suspendu (Sⁿ A, a ⁿ ) de (A, a ). Une généralisation de la suite spectrale des fibrés donne d’intéressantes relations entre l’homotopie de A et celle de SA; on démontre en particulier le théorème de Freudenthal : Si A est connexe, alors on a, respectivement pour i 麗 n et pour i 諒 2n 漣 2:

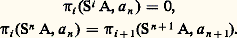Classification

Soit 﨏: YB un fibré de fibre F; pour toute application 見: CB, notons Z size=1^見 le sous-espace de C 憐 Y formé des points (c , y ) tels que 見(c ) = 﨏(y ); l’application 祥 de Z size=1^見 dans C définie par 祥(c , y ) = c est une fibration de fibre F. Si la fibration 﨏: YB est localement triviale, alors 祥: Z size=1^見C l’est aussi; si la fibration 﨏: YB est munie d’un groupe structural G, il en est de même de 祥: Z size=1^見C. On dit que 祥: Z size=1^見C est l’image inverse de 﨏: YB par l’application 見. On démontre que, si les applications 見 et 廓 de C dans B sont homotopes et si C est assez simple, par exemple si c’est un polyèdre, les fibrés images réciproques par 見 et 廓 sont isomorphes.

Pour tout fibré 﨏: YB de fibre F muni du groupe structural G, la construction précédente définit donc une application de l’ensemble des classes d’homotopie d’applications de C dans B dans l’ensemble des classes à isomorphisme près de fibrés de base C, de fibre F et de groupe structural G. Dans la plupart des cas (en particulier si g est un groupe de Lie, donc dans le cas des fibrés vectoriels de fibre Rⁿ ou Cⁿ et de groupe GL(n , R) ou GL(n , C)), il existe un fibré 﨏: YB tel que, pour tout polyèdre C, cette application soit une bijection. Ce fibré 﨏: YB est appelé le fibré universel , ou fibré classifiant , de fibre F et de groupe structural G. On démontre que, dans le cas des fibrés principaux, tous les groupes d’homotopie de Y sont nuls.

5. Autres développements

Fibrés vectoriels stables

Soit E et F deux fibrés vectoriels réels de base X, c’est-à-dire deux fibrés localement triviaux dont la fibre est un espace vectoriel sur R (sa dimension est appelée la dimension du fibré) et dont le groupe structural est le groupe des isomorphismes linéaires de cette fibre. On définit un fibré vectoriel réel E 簾 F, appelé somme de E et de F, dont la fibre en un point x est la somme directe des fibres en x de E et de F; ce fibré a donc pour dimension la somme des dimensions de E et de F. Si E est le fibré trivial X 憐 R^pX, la somme de E et de FX est le fibré R^p 憐 FX.

On dit que deux fibrés ⁰ et ¹ de base X sont stablement équivalents s’il existe des fibrés triviaux E⁰ et E¹ de base X tels que E⁰ 簾 ⁰ et E¹ 簾 ¹ soient isomorphes. Cette notion de classe stable d’un fibré a été introduite en topologie différentielle pour l’étude des fibrés normaux aux variétés (cf. TOPOLOGIE – Topologie différentielle, chap. 5); elle a ensuite pris une grande importance dans le développement de la topologie algébrique moderne.

On note KO(X) l’ensemble des classes stables de fibrés vectoriels réels de base X. La somme des fibrés induit une loi de composition sur KO(X); si X est compact (ou si X est un polyèdre), c’est une loi de groupe abélien. On définit de même le groupe K(X) des classes stables de fibrés vectoriels complexes de base X.

Foncteurs homologiques généralisés

Un théorème de R. Bott affirme que K(X) est isomorphe à K(S²X), en désignant par S²X la seconde suspension de X; de même KO(X) est isomorphe à KO(S⁸X). Cela permet de définir une famille de foncteurs Kⁱ (X) et KOⁱ (X) très analogues aux groupes de cohomologie (cf. infra , Cohomologie ); ce sont les premiers exemples connus des «théories cohomologiques (ou homologiques) généralisées», qui constituent l’un des principaux domaines de la topologie algébrique. Une étude systématique de ces théories homologiques a été entreprise avec la S-théorie et les suites spectrales d’Adams.

Parmi les recherches, on doit signaler aussi l’étude des foncteurs représentables et des structures algébriques dans la catégorie des espaces topologiques et des classes d’homotopie d’applications.

6. Algèbre homologique

Homologie d’un module différentiel

Considérons une famille (Mⁿ ), avec n 捻 Z, de A modules et, pour tout n , une application d ⁿ de Mⁿ dans M^{n +} size=1^﨎, où 﨎 est un entier en général égal à + 1 ou à 漣 1. Si, pour tout n , on a:

on dit que face=F9796 M = ((Mⁿ ), (d ⁿ )), pour n 捻 Z, est un A-module différentiel gradué ; les d ⁿ sont appelés les opérateurs bord de face=F9796 M. Toute suite exacte infinie: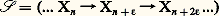

de A-modules est un A-module différentiel gradué; mais, en général, un A-module différentiel gradué n’est pas une suite exacte; on introduit son homologie pour mesurer en quoi ce n’en est pas une. On appelle cycle de dimension n les éléments du noyau Zⁿ de d ⁿ ; on appelle bords de dimension n les éléments de l’image Bⁿ de d ⁿ size=1^漣 size=1^﨎. Pour tout n , le module Bⁿ est un sous-module de Zⁿ ; le module quotient de Zⁿ par Bⁿ est appelé le module d’homologie en dimension n de face=F9796 M. On le notera Hⁿ (face=F9796 M).

Soit face=F9796 M=((Mⁿ ), (d ⁿ )) et face=F9796 L=((Lⁿ ), ( 嗀ⁿ )) deux A-modules différentiels gradués; si, pour tout n , on s’est donné un homomorphisme 見ⁿ : MⁿLⁿ , de telle façon que l’on ait:

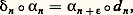on dit que 見 = ( 見ⁿ ), pour n 捻 Z, est un morphisme de face=F9796 M dans face=F9796 L. L’image par 見ⁿ d’un cycle (resp. d’un bord) de dimension n de face=F9796 M est un cycle (resp. un bord) de dimension n de face=F9796 L; donc 見 induit, pour tout n , un homomorphisme Hⁿ ( 見) de Hⁿ (face=F9796 M) dans Hⁿ (face=F9796 L). Cela permet de dire que l’homologie est un foncteur de la catégorie des modules différentiels gradués dans celle des modules gradués.

Supposons maintenant que 見ⁿ soit injectif quel que soit n ; on définit un A-module différentiel gradué face=F9796 L/ face=F9796 M de la façon suivante: pour tout n , on considère le A-module Lⁿ /Mⁿ et on applique l’homomorphisme:

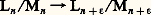en associant à la classe deⁿ 捻 Lⁿ celle de 嗀ⁿ (ⁿ ) 捻 Lⁿ⁺ size=1^﨎. L’homologie de face=F9796 L/ face=F9796 M s’appelle l’homologie relative de face=F9796 L modulo face=F9796 M; on la note (Hⁿ (face=F9796 L, face=F9796 M)), avec n 捻 Z. L’application naturelle LⁿLⁿ /Mⁿ définit un morphisme de modules différentiels qui, pour tout n , induit un homomorphisme:

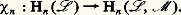Pour tout cycle de dimension n de face=F9796 L/ face=F9796 M, il existe un élément y de Lⁿ dont la classe est x . L’élément 嗀ⁿ (y ) est l’image d’un élément z de Mⁿ⁺ size=1^﨎 et cet élément z est un cycle de face=F9796 M de dimension n + 﨎. En associant à celle de x la classe d’homologie de z , on définit un homomorphisme:

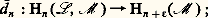on démontre que, quel que soit n , la suite:

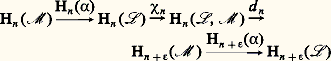est exacte.

Toutes ces constructions ont des propriétés fonctorielles évidentes que l’on ne peut détailler ici.

Suites spectrales

Supposons que le module différentiel gradué face=F9796 M soit la réunion d’une famille croissante (face=F9796 M^p ), avec p 捻 Z, de modules différentiels gradués; on dit alors que face=F9796 M est un module différentiel gradué filtré. Il arrive très souvent que l’on connaisse l’homologie des face=F9796 M^p / face=F9796 M^{p -1} et que l’on cherche à calculer celle de face=F9796 M. La suite spectrale de face=F9796 M est une famille de modules différentiels gradués:

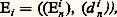pour i 閭 1, telle que, pour tout i 閭 2, les modules E^{i n} soient l’homologie de E^{i -1} et que l’homologie de face=F9796 M soit, en un certain sens, la limite des Eⁱ . Les modules E²ⁿ sont assez bien connus si l’on peut calculer l’homologie des face=F9796 M^p / face=F9796 M^{p -1}; malheureusement, on ne connaît en général pas l’opérateur bord (d ²ⁿ ) et on ne connaît donc pas non plus les E ⁱ pour i 閭 3. Cependant, dans certains cas particuliers, on peut mener les calculs jusqu’au bout. La suite spectrale est l’un des plus féconds des outils de l’algèbre homologique.

Foncteurs dérivés

Soit A un anneau commutatif; pour tout couple ( 炙, M) de A-modules, l’ensemble Hom^A ( 炙, M) des homomorphismes de 炙 dans M est muni, de manière naturelle, d’une structure de A-module. On associe à tout homomorphisme 﨏: MN un homomorphisme:

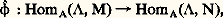où 﨏( 見) est l’homomorphisme 﨏 獵 見: 炙N pour tout 見: 炙M, ce qui fait de Hom^A( 炙, .) un foncteur de la catégorie des A-modules dans elle-même. Si la suite:

est exacte, la suite:

l’est aussi, mais 祥 n’est en général pas surjectif. On exprime ce fait en disant que le foncteur Hom^A ( 炙, .) n’est pas exact, mais qu’il est seulement semi-exact. Si 炙 est tel que, quelle que soit la suite exacte: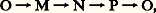

l’homomorphisme 祥 soit surjectif, on dit que 炙 est un A-module projectif . Tous les A-modules libres sont projectifs et, en particulier, si A est un corps, tous les A-modules sont projectifs.

On introduit, pour tout i 閭 1, des foncteurs Ext^{i A} ( 炙, .) tels qu’à toute suite exacte:

corresponde une suite exacte infinie: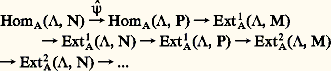

Le module Ext^1A ( 炙, M) permet donc, en quelque sorte, de mesurer «de combien» 祥 n’est pas surjectif; il est nul si M est projectif. Les modules Ext^{i A} sont appelés les foncteurs dérivés du foncteur Hom^A ( 炙, .); pour calculer les modules Ext^{i A} ( 炙, M), on construit une suite exacte infinie:

où les Lⁱ sont libres et on prend l’homologie du A-module différentiel gradué ((Hom^A ( 炙, Lⁱ )), (face=F0019 煉ⁱ )). Si l’on connaît l’homologie du module différentiel gradué face=F9796 M = ((Mⁿ ), (d ⁿ )), les foncteurs Ext^{i A} permettent de calculer l’homologie du A-module différentiel gradué:

7. Faisceaux

La notion de faisceau fut introduite vers 1950 par J. Leray et H. Cartan pour formaliser un certain nombre de théorèmes de topologie algébrique. Vingt ans plus tard, elle jouait un rôle à peu près nul en topologie; mais elle fait partie du langage naturel de la géométrie algébrique et de la géométrie analytique (cf. FONCTIONS ANALYTIQUES Fonctions analytiques de plusieurs variables complexes, GÉOMÉTRIE ALGÉBRIQUE).

La notion de faisceau

Considérons une application continue p : YX et, pour tout ouvert U de X, notons face=F9796 ^U l’ensemble des sections de p au-dessus de U, c’est-à-dire l’ensemble des applications continues s : UY telles que p 獵 s soit l’application identique de U. Pour U 說 U, à tout élément s de face=F9796 ^U on associe sa restriction s ^|U size=1 à U ; ce qui définit une application de face=F9796 ^U dans face=F9796 U . Il est clair que les deux propriétés suivantes sont vérifiées.

a ) Si U 說 U 說 U et si s est un élément de face=F9796 ^U, on a: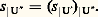

b ) Si U est la réunion des ouverts Uⁱ , si, pour tout i , s ⁱ est un élément de face=F9796 ^Ui et si, pour tout couple (i , f ), on a:

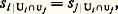alors il existe un élément s et un seul de face=F9796 ^U tel que, pour tout i , on ait s ^|Ui = s ⁱ (condition de recollement).

On dit alors que les face=F9796 ^U et les applications de restriction forment le faisceau des sections de p . Plus généralement, chaque fois que l’on se sera donné, pour tout ouvert U de X, un ensemble face=F9796 G^U et, pour tout U contenu dans U, une application de face=F9796 G^U dans face=F9796 GU , que l’on appellera restriction, de façon que les propriétés a et b soit vérifiées, on dira que l’on a un faisceau face=F9796 G de base X.

Exemples

1. Soit p la seconde projection du produit A 憐 X; le faisceau des sections de p est encore appelé le faisceau des fonctions continues à valeurs dans A.

2. Soit X une variété différentiable et soit p la projection de l’espace tangent à X; une section, au-dessus de U, du faisceau face=F9796 associé à p est un champ de vecteurs défini sur U.

3. Les deux exemples précédents sont donnés comme des faisceaux de sections d’une application p à valeurs dans X; il n’en est pas toujours ainsi. Associons, par exemple, à chaque ouvert U de la variété X l’ensemble 行^{k U} des formes différentielles de degré k définies sur U. On obtient le faisceau 行^k des formes différentielles de degré k sur la variété X.

En général, comme dans les exemples 2 et 3, les face=F9796 ^U sont munis d’une structure algébrique (groupe, anneau, A-module, etc.) et les restrictions sont des homomorphismes de cette structure; on dit alors que l’on a un faisceau de groupes, d’anneaux, de A-modules, etc.

Si face=F9796 et face=F9796 G sont deux faisceaux de base X, un morphisme 見 de face=F9796 dans face=F9796 G est la donnée, pour tout ouvert U de X, d’une application 見^U de face=F9796 ^U dans face=F9796 G^U, de telle façon que, chaque fois que U est contenu dans U et que f est un élément de face=F9796 ^U, on a:

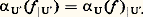Par exemple, si à toute forme différentielle 諸 de degré k sur l’ouvert U de la variété X on associe sa différentielle, on obtient un morphisme du faisceau 行^k dans le faisceau 行^{k +1}. Si face=F9796 et face=F9796 G sont des faisceaux de groupes (resp. d’anneaux, de A-modules, etc.), on impose aux 見^U d’être des homomorphismes de groupes (resp. d’anneaux, de A-modules, etc.) et on dit que 見 est un morphisme de faisceaux de groupes (resp. d’anneaux, de A-modules, etc.).

Exactitude

Soit face=F9796 F 見face=F9796 G 廓face=F9796 H une suite d’homomorphismes de faisceaux de groupes (ou d’anneaux, ou de A-modules) de base X; on dit que cette suite est exacte si:

a ) Pour tout ouvert U de X, on a:

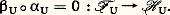b ) Pour tout élément g de face=F9796 G^U tel que 廓^U(g ) = 0 et tout point x de U, il existe un voisinage U de x dans U et un élément f de U tel que:

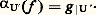Par exemple, pour toute variété X, la suite:

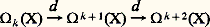est exacte alors, car toute forme fermée est localement intégrale; on remarque (c’est clair sur cet exemple) que, pour un ouvert U quelconque, la suite:

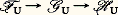n’est pas exacte. On peut cependant démontrer que, si la suite:

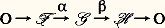est exacte, pour tout ouvert U, la suite:

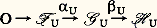est exacte; mais 廓^U n’est en général pas surjective.

Cohomologie

On considère le cas où on a U = X et on va donner des conditions suffisantes pour que 廓^U soit surjective; curieusement, ces conditions portent uniquement sur face=F9796 et non sur face=F9796 G et face=F9796 H.

Supposons que face=F9796 vérifie la condition suivante: Pour tout ouvert U de X et tout élément 見 de face=F9796 ^U, il existe un élément 廓 de face=F9796 ^X tel que 廓^|U = 見; on dit alors que face=F9796 est un faisceau fin . On vérifie facilement que, si face=F9796 est fin, la suite:

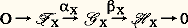est exacte. On rencontre peu de faisceaux fins; cependant, il en existe assez pour qu’on puisse associer à tout faisceau 杻 de base X une suite exacte infinie:

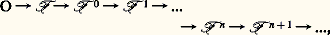dans laquelle tous les face=F9796 Fⁱ sont fins. La suite:

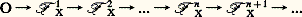n’est en général pas exacte; c’est un groupe différentiel gradué. Son homologie ne dépend pas de la famille (face=F9796 Fⁱ ) choisie; elle ne dépend que de face=F9796 ; c’est la cohomologie de X à valeurs dans le faisceau face=F9796 et on la note (Hⁿ (X, face=F9796 )), pour n 閭 0.

Le groupe H⁰(X, face=F9796 ) est naturellement isomorphe à face=F9796 ^X. À toute suite exacte:

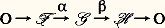on associe une suite exacte infinie:

Pour que 廓^X soit surjectif, il suffit donc que H¹(X, face=F9796 ) soit nul.

Encyclopédie Universelle. 2012.